The alpha question became the alpha conjecture

The alpha question . Let be a prime (greater than 3, to prevent it from being 3) such that

• (the ' -1' case) and are both prime, or
• (the '+1' case) and are both prime

is it then true that 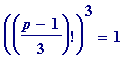(mod p )?

(Private terminology . I took to calling the other primes ' inexplicable ' for the time being. Other later examples, when I extended my searching were: 25117 - 1 = ( ) (3) (7) (13) (23), 60919 - 1 = (2) (3) (11) (13) (71),

92401 - 1 = ( ) (3) ( ) (7) (11), 115827 - 1 =( ) (3) ( ) (197), etc etc. )

There were two first cases to examine, with unimportant order: with '+1' or '-1'.

Let's say we begin, as I did, with and '-1': thus we are trying to find primes { p } made up as follows:

, where are primes with , ( )

and are hoping that such primes satisfy:

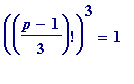(mod p )

Such p 's are like this:

=

which is, as I observed at the time, a quadratic whose discriminant is

Here I show and '-1' for forming some primes { p }.

I abbreviate 'alpha' to 'a' in the following to reduce the program lines in the following, in which:

• ithprime(k) is the ithprime, 'k' starting at 3 ("from 3"): 5, 7, 11, 13, 17, ...
  So, that produces the candidates for
• isprime(2^a*ithprime(k)+SIGN) produces the candidates 2^a*ithprime(k)+SIGN for
• isprime(2^a*3*ithprime(k)*(2^a*ithprime(k)+SIGN)+1) produces the desired primes { p },
  the 2^a*3*ithprime(k)*(2^a*ithprime(k)+SIGN)+1

> a := 1: SIGN := -1:
count:= 0: for k from 3 to 100 do
if isprime(2^a*ithprime(k)+SIGN) and isprime(2^a*3*ithprime(k)*(2^a*ithprime(k)+SIGN)+1) then count := count+1:
q1[count] := ithprime(k):
q2[count] := 2^a*q1[count]+SIGN:
p[count] := 2^a*3*q1[count]*q2[count]+1:
fi od;
array([[q[1], q[2], p], seq([q1[k], q2[k], p[k]], k=1..count)]);

>

At the time at which I tested the above, I had systematically tested for 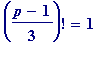(mod p ), for all primes up to the 30,000th (note to myself: all that is saved in a Maple worksheet that I had called ' Wilson play .mws', the name of which gives an indication of my attitude up until then). The largest such prime p I had found at that stage had been 347821 (an 'inexplicable' prime, being *3*5*11*17*31), and thus those three last new primes - 627919, 879667, and 2310019 - in the above table were first tester candidates of my alpha observation ... ( heart beating... ).

Well, I wouldn't be here talking to you if it hadn't turned out that:

> p1 := 627919: P[1,3](p1) mod p1; # didn't produce a '1'

> 1372^3 mod p1; # but its cube did

> p2 := 879667: P[1,3](p2) mod p2;

> p3 := 2310019: P[1,3](p3) mod p3;

>

The reader may imagine how I felt seeing those 1's...

> a := 1: SIGN := -1:
count:= 0: for k from 501 to 1000 do
if isprime(2^a*ithprime(k)+SIGN) and isprime(2^a*3*ithprime(k)*(2^a*ithprime(k)+SIGN)+1) then count := count+1:
q1[count] := ithprime(k):
q2[count] := 2^a*q1[count]+SIGN:
p[count] := 2^a*3*q1[count]*q2[count]+1:
fi od;
array([[q[1], q[2], p], seq([q1[k], q2[k], p[k]], k=1..count)]);

>

Here I show and '+1' for forming some primes { p }:

> a := 1: SIGN := +1:
count:= 0: for k from 3 to 100 do
if isprime(2^a*ithprime(k)+SIGN) and isprime(2^a*3*ithprime(k)*(2^a*ithprime(k)+SIGN)+1) then count := count+1:
q1[count] := ithprime(k):
q2[count] := 2^a*q1[count]+SIGN:
p[count] := 2^a*3*q1[count]*q2[count]+1:
fi od;
array([[q[1], q[2], p], seq([q1[k], q2[k], p[k]], k=1..count)]);

>

I tested alpha up to 10 with both '-1' and '+1' choices, and checked if 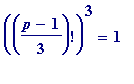(mod p ) held, not for all the produced primes { p }, but only because of computation time constraints : for example, the prime 18711862657 (see below: , , ) took 80.5 hours to test on a 2.8GHz Pentium 4 .

Here I show and '+1' for forming some primes { p }:

> a := 7: SIGN := +1:
count:= 0: for k from 3 to 200 do
if isprime(2^a*ithprime(k)+SIGN) and isprime(2^a*3*ithprime(k)*(2^a*ithprime(k)+SIGN)+1) then count := count+1:
q1[count] := ithprime(k):
q2[count] := 2^a*q1[count]+SIGN:
p[count] := 2^a*3*q1[count]*q2[count]+1:
fi od;
array([[q[1], q[2], p], seq([q1[k], q2[k], p[k]], k=1..count)]);

>

Of course I knew I was onto something:

The alpha conjecture. Let be a prime (greater than 3, to prevent it from being 3) such that

• (the ' -1' case) and are both prime, or
• (the '+1' case) and are both prime

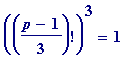then (mod p )

But the problem then became: how can one prove this ( almost certainly tru e) conjecture? That brings me to the next natural section: